
by Richard E. | Aug 7, 2023 | Research
Standard cosmological scenarios propose that the Big Bang was followed immediately by a period of accelerated expansion, or inflation. Inflaton has two roles in shaping the Universe. First and foremost, the rapid growth stretches everything in the early Universe and...

by Richard E. | Aug 1, 2023 | Research
For astronomers, looking at the sky can be like watching an unfamiliar sport on TV. We can’t make sense of what we see, but is it because we don’t know the rules, or that we can’t see all the players? (Or, worst case, we can’t see the players...
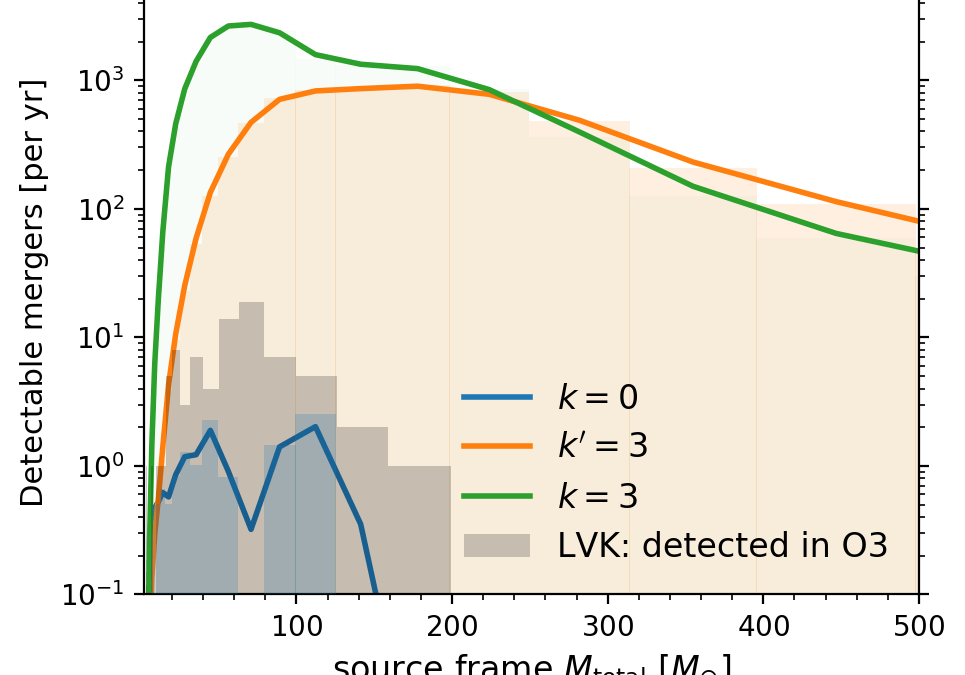
by Richard E. | Jul 1, 2023 | Research
A recent paper made the somewhat surprising claim that black holes in an expanding universe are “cosmologically coupled” — that is, their mass increases as the Universe expands, to the point that the density of a population of black holes would stay...

by Richard E. | Jan 29, 2023 | Research
If the visible universe starts out at the Planck scale it must have grown larger by at least 60 factors of 10 since the Big Bang. Half of these “decades” of expansion would be accounted for by the hypothetical inflationary phase, a period of accelerated...

by gcas520 | Jul 12, 2018 | Research, Resources
In the simplest models (and thus best-studied) models, gravity is the only interaction that plays a role in the overall astrophysical predictions of the dark matter. However, many models that have interesting connections to particle physics have more complicated...





